MICROCAVIDADES
YMULTICAPAS COMPLEJAS
|
En los cristales fotónicos
unidimensionales se pueden introducir defectos que rompen la simetría.
Por ejemplo puede incorporarse en el medio de la multicapa una única capa
con un espesor óptico diferente de las demás, como se muestra en la
figura de la derecha. De esta forma resulta una cavidad que separa dos
reflectores de Bragg, que puede funcionar como un interferómetro de Fabry-Perot.
En la fotomicrografía de abajo (izquierda)
puede verse en corte la estructura de una microcavidad de este tipo en la
que se observan las capas de diferente porosidad . A la derecha se observa
en detalle la estructura porosa de una sola capa, cuyo crecimiento tiene
una dirección preferencial. |

|
|
Esquema del
corte de una microcavidad |
|

|
|
 |
|
Fotomicrografía
del corte de una microcavidad óptica con reflectores de Bragg
de 8 pares de capas. Fué obtenida por Claudia Marchi en el Microscopio
electrónico de barrido por emisión de campo del CMA de la Facultad de
Ciencias Exactas de la Universidad de Buenos Aires. |
|
Fotomicrografía de
una de las capas de la microcavidad óptica. Se observa la dirección
preferencial de la estructura segun la dirección <100>, asi como
una característica dendritica del mismo. |
|
|
|
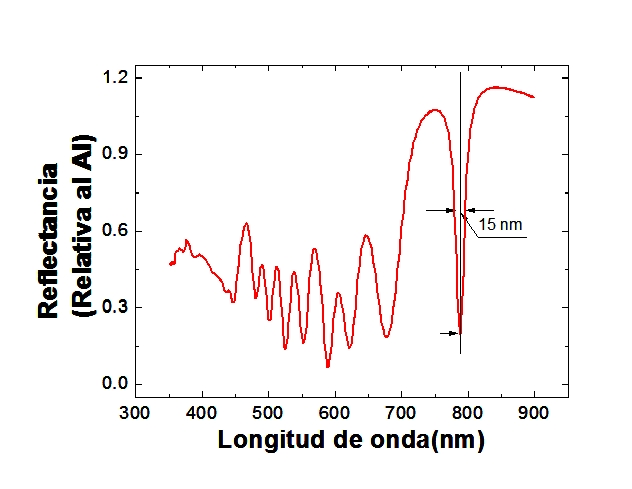
Espectro de una
microcavidad óptica cuyo defecto tiene un espesor óptico igual a l0/2.
Se observa una resonancia muy aguda en el centro del gap óptico. Este
dispositivo funciona como un filtro de interferencia (debería eliminarse
el sustrato que no es transparente). Una pequeña modificación causada
por ajentes presentes en la atmósfera se traduce en una gran variación
de la reflectancia para la longitud de onda correspondiente a la
resonancia (pasar el mouse por la figura para ver el efecto). De este modo
se pueden obtener mayores sensibilidades en los sensores basados en
propiedades fotónicas.
|
 |
 |
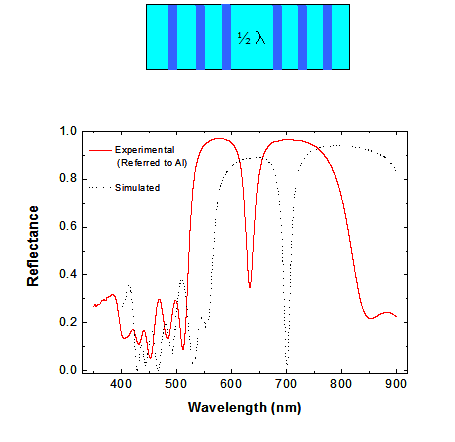
Arriba: Espectros de
cavidades ópticas. A la izquierda se observa una cavidad simple con un defecto
de 1/2 l0,
cuyo esquema se observa en corte arriba del gráfico. En rojo, línea llena se
observa el espectro experimental, y en línea de puntos, en negro se observa la
simulación basada en las propiedades ópticas medidas en películas simples. El
desfasaje observado se debe principalmente a efectos de polarización que
ocurren porque los cambios de concentración del electrolito dentro de la
estructura porosa no acompañan a los cambios rápidos de densidad de corriente.
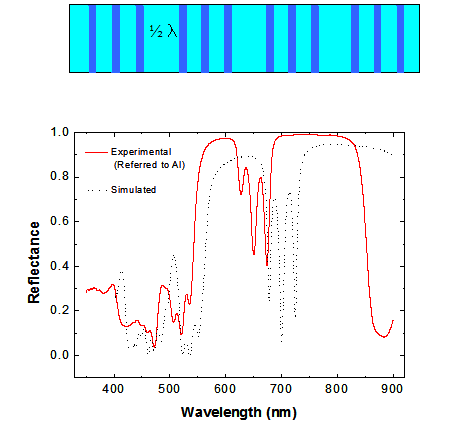
A la derecha se observa el espectro de una cavidad triple con defecto del mismo
ancho, cuyo esquema se muestra en corte arriba. En lugar de una única
resonancia en el centro del gap se observa un triplete. El desdoblamiento se
debe a efectos de acoplamiento. Si se introducen mas defectos a intervalos
regulares se multiplica el desdoblamiento, y para un gran número de defectos en
una estructura regular se obtiene una banda anch dentro del gap, en lugar de la
resonancia inicial.
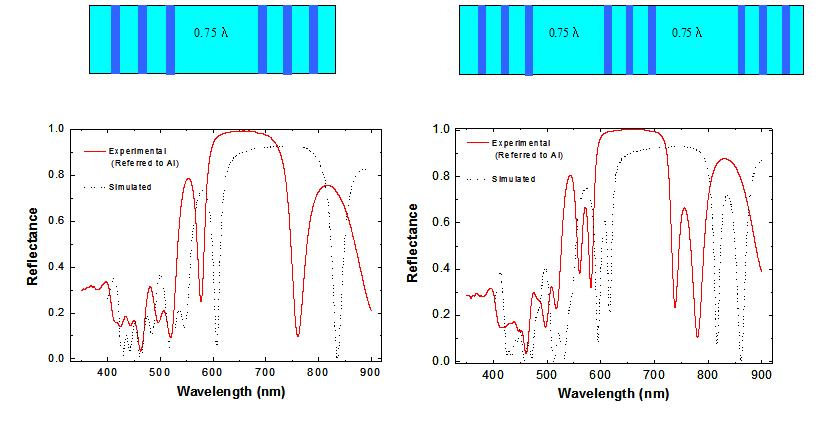
Arriba: El acoplamiento en
cavidades múltiples no es el único modo de obtener resonancias múltiples. Si
se introducen defectos de ditinto espesor, la resonancia se corre (hacia el azul
para cavidades entre 1/4 y 1/2 de l0 y
hacia el rojo para espesores mayores. Eventualmente, si se aumenta
suficientemente el espesor del defecto, aparecen nuevas resonancias. En el
ejemplo se observa a la izquierda el espectro de una cavidad con defecto de 0.75
l0. A la derecha se observan los efectos
de acoplamiento en una cavidad doble con el mismo tamaño de defecto. Notar de
nuevo el desplazamiento hacia el azul respecto del espectro simulado. Los
esquemas de arriba muestran en corte la estructura de las microcavidades
.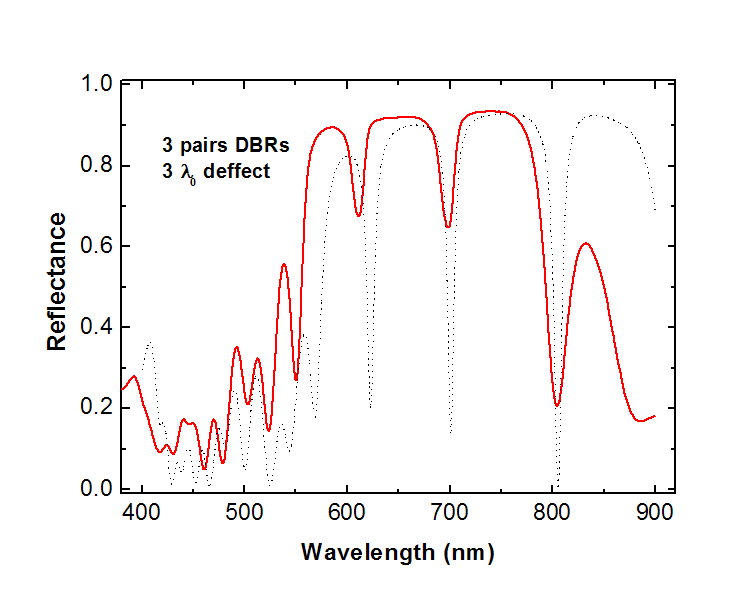
Arriba: Espectro de una
microcavidad simple con defecto de espesor óptico igual a 3 l0.
Se observan varias resonancias dentro del gap fotónico.







