MICROCAVIDADES
Y MULTICAPAS COMPLEJAS, SENSORES
|
En los cristales fotónicos
unidimensionales se pueden introducir defectos que rompen la simetría.
Por ejemplo puede incorporarse en el medio de la multicapa una única capa
con un espesor óptico diferente de las demás, como se muestra en la
figura de la derecha. De esta forma resulta una cavidad que separa dos
reflectores de Bragg, que puede funcionar como un interferómetro de Fabry-Perot.
En la fotomicrografía de abajo (izquierda)
puede verse en corte la estructura de una microcavidad de este tipo en la
que se observan las capas de diferente porosidad . A la derecha se observa
en detalle la estructura porosa de una sola capa, cuyo crecimiento tiene
una dirección preferencial. |

|
|
Esquema del
corte de una microcavidad |
|

|
|
 |
|
Corte de una microcavidad óptica con reflectores de Bragg
de 8 pares de capas, preparada en nuestro Laboratorio. La
fotomicrografía fue obtenida por Claudia Marchi en el microscopio
electrónico de barrido por emisión de campo del CMA de la Facultad de
Ciencias Exactas de la Universidad de Buenos Aires. |
|
Fotomicrografía de
una de las capas de la microcavidad óptica mostrada a la izquierda. Se observa la dirección
preferencial de la estructura segun la dirección <100> del sustrato
de silicio, asi como
una característica dendritica de la misma. |
|
|
|
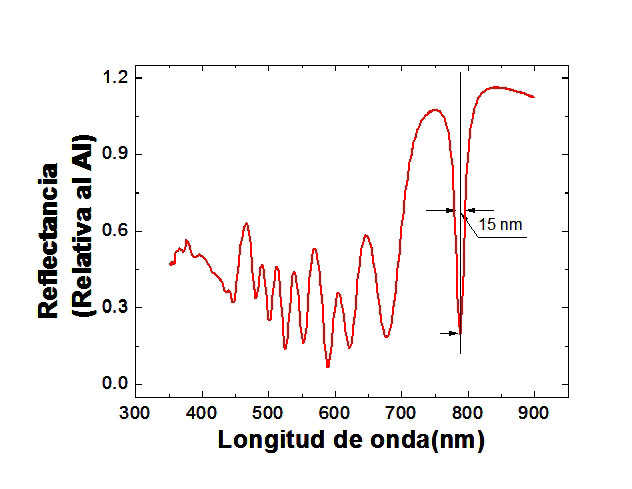
Arriba:
Espectro de una
microcavidad óptica cuyo defecto tiene un espesor óptico igual a l0/2.
Se observa una resonancia muy aguda en el centro del gap óptico. Este
dispositivo funciona como un filtro de interferencia. Para obtener un
filtro por transmisión debe eliminarse
el sustrato que no es transparente, lo cual puede hacerse usando un pulso
de alta corriente al final de la preparación. Este tipo de dispositivos
ya fue fabricado en nuestro laboratorio. Una pequeña modificación causada
por agentes presentes en la atmósfera se traduce en una gran variación
de la reflectancia para la longitud de onda correspondiente a la
resonancia . De este modo
se pueden obtener mayores sensibilidades en los sensores basados en
propiedades fotónicas.
|
 |
 |
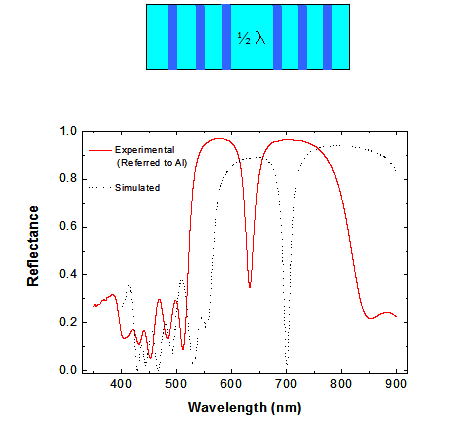
Arriba:
Espectros de
cavidades ópticas. A la izquierda se observa una cavidad simple con un defecto
de 1/2 l0,
cuyo esquema se observa en corte arriba del gráfico. En rojo, línea llena se
observa el espectro experimental, y en línea de puntos, en negro se observa la
simulación basada en las propiedades ópticas medidas en películas simples. El
desfasaje observado se debe en parte a efectos de polarización que
ocurren porque los cambios de concentración del electrolito dentro de la
estructura porosa no acompañan a los cambios rápidos de densidad de corriente,
lo que puede corregirse usando "tiempos muertos" sin suministro de
corriente entre capa y capa.
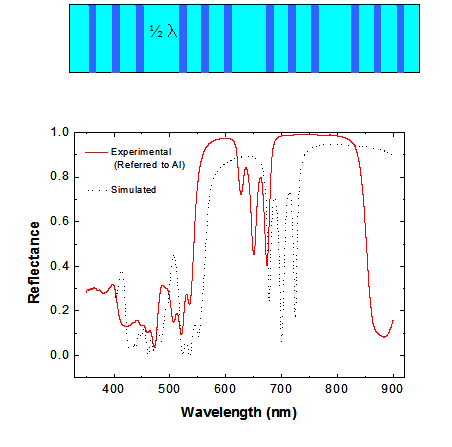
A la derecha se observa el espectro de una cavidad triple con defecto del mismo
ancho que la correspondiente a la figura de la izquierda. El esquema se muestra en corte arriba. En lugar de una única
resonancia en el centro del gap se observa un triplete. El desdoblamiento se
debe a efectos de acoplamiento. Si se introducen mas defectos a intervalos
regulares se multiplica el desdoblamiento, y para un gran número de defectos en
una estructura regular se obtiene una banda anch dentro del gap, en lugar de la
resonancia inicial.
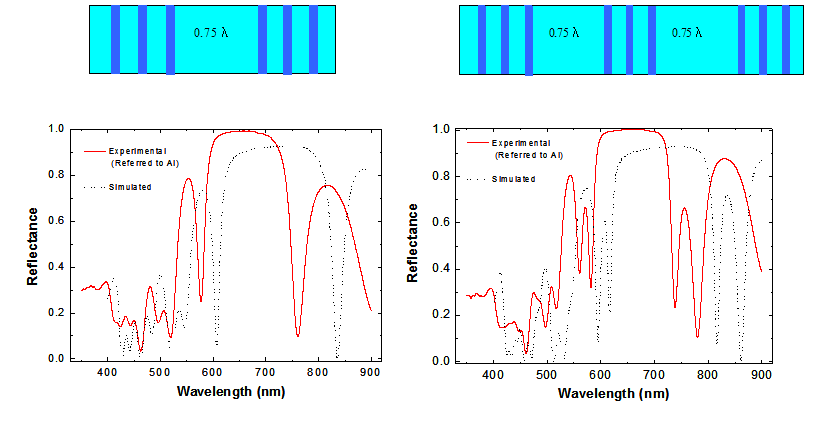
Arriba:
El acoplamiento en
cavidades múltiples no es el único modo de obtener resonancias múltiples. Si
se introducen defectos de ditinto espesor, la resonancia se corre (hacia el azul
para cavidades entre 1/4 y 1/2 de l0 y
hacia el rojo para espesores mayores. Eventualmente, si se aumenta
suficientemente el espesor del defecto, aparecen nuevas resonancias. En el
ejemplo se observa a la izquierda el espectro de una cavidad con defecto de 0.75
l0. A la derecha se observan los efectos
de acoplamiento en una cavidad doble con el mismo tamaño de defecto. Notar de
nuevo el desplazamiento hacia el azul respecto del espectro simulado. Los
esquemas de arriba muestran en corte la estructura de las microcavidades
.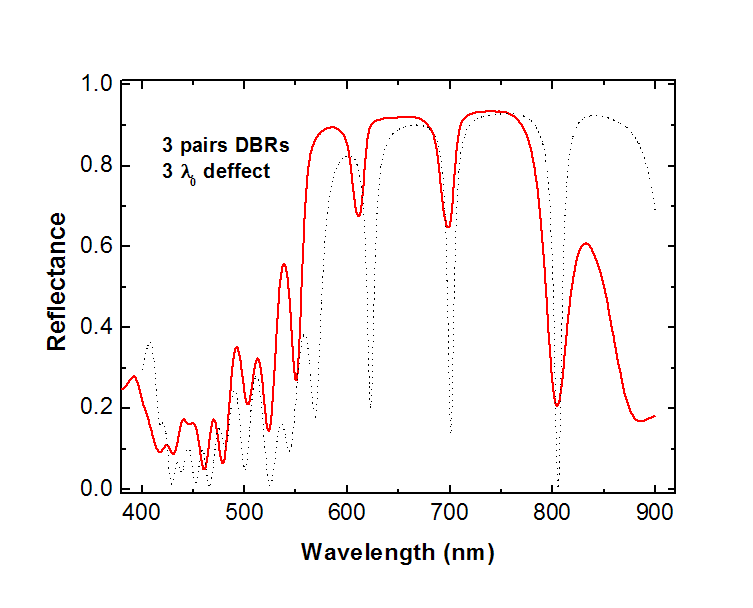
Arriba:
Espectro de una microcavidad simple con defecto de espesor óptico igual
a 3 l0. Se observan
varias resonancias dentro del gap fotónico.
 |
El silicio
monocristalino es un material de gap indirecto. Esto significa que la base
de la banda de conducción no coincide en el espacio de k con el tope de
la banda de valencia, y por tanto las transiciones radiativas entre ambas
son muy improbables, debido a que precisan del intercambio de fonones para
conservar el momento. Además el gap del silicio es de 1.1 eV, por lo que la
fotoluminiscencia (naturalmente poco eficiente por lo antedicho) ocurre en
el infrarrojo.
Cuando se producen
estructuras en una escala nanoscópica como en el caso del silicio poroso,
ocurren dos efectos de naturaleza cuantica: por un lado, la banda
prohibida se agranda como consecuencia de efectos de confinamiento
cuántico, de modo que la emisión se produce a una energia mayor que
puede ser controlada a través del tamaño de la nanoestructura. Por otro
lado, debido al principio de incerteza, se ensanchan las bandas en el
espacio de k por lo que se relaja la regla de selección del cuasimomento,
y la emisión es entonces mucho más eficiente.
En la figura se
obselva arriba la luminiscencia de una muestra preparada en nuestro
laboratorio cuando se la ilumina con luz de 400 nm de longitud de onda. La
imagen de abajo corresponde a la misma muestra iluminada con luz visible.
La longitud de onda
de De Broglie de los electrones en el silicio es del orden de 5 nm. por lo
que los efectos de confinamiendo se producen eficientemente cuando
aparecen estructuras menores. En el caso de la muestra ilustrada, el
espectro de luminiscencia corresponde a una estructura formada por
nanoalambres de un diámetro medio de 2.4 nm. |
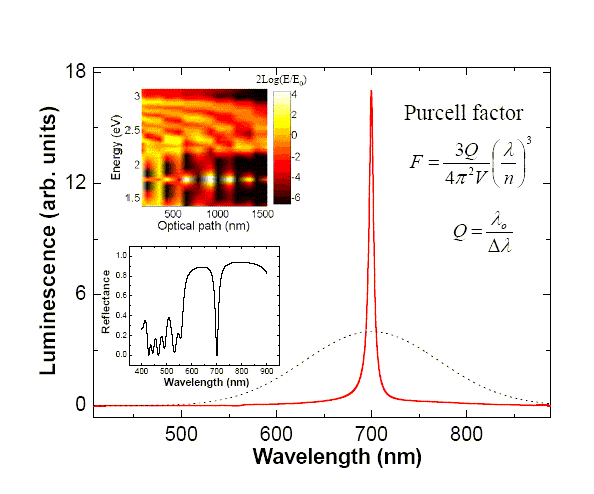
Arriba:
el espectro de luminiscencia del silicio poroso es ancho, como se muestra en
linea de puntos en la figura. Sin embargo, cuando el campo se confina en una
región, la emisión estimulada resulta afectada por un factor denominada
"Factor de Purcel" cuya expresión se indica en la figura, (Q es el
factor de calidad y V es el "volumen del modo", que cuantifica el
confinamiento del campo. En una microcavidad como las mencionadas anteriormente,
cuyo espectro de reflexión simulado se muestra en negro en la imajen insertada inferior, la
intensidad de campo se comporta como se muestra en la imágen insertada
superior: la tabla de colores representa en escala logaritmica la intensidad de
campo en unidades del campo incidente. Se puede apreciar una zona oscura entre
1.5 y 2.2 eV en la que el campo es pequeño pudiendo llegar a ser 10-6
veces menor que el campo incidente. Sin embargo, en la resonancia el campo
aumenta hasta valores que superan en 104 veces el campo incidente.
Como consecuencia el espectro de emisión del silicio poroso confinado en una
microcavidad presenta un espectro mucho mas agudo, y con un valor maximo mayor
que el correspondiente a una película simple. En rojo se representa dicho
espectro, como resultado de una simulación realizada para el caso de la
microcavidad indicada (la intensidad se ha reducido en dos ordenes de magnitud a
efectos de visualizar el espectro de línea de puntos). Este efecto puede ser
usado para utlizar la luminiscencia como propiedad adecuada para sensores, como
se muestra en la figura siguiente.
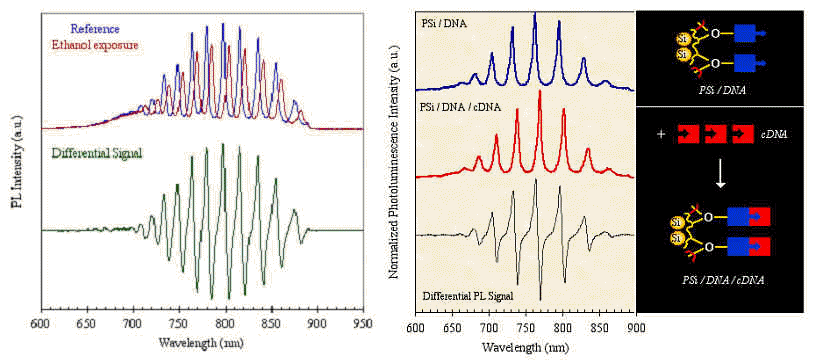
Arriba:
la luminiscencia usada como medio para sensores químicos y biosensores: a la
izquierda, una cavidad con defecto grande presenta muchos picos, cuya envolvente
resembla el espectro de luminiscencia del silicio poroso en película simple.
Cuando se expone esta muestra a un agente que cambia el índice de refracción
se producen cambios en la posición de las resonancias, que son fácilmente
medibles a través del espectro diferencia, debido a lo agudo de los picos.
A
la izquierda se muestra el comportamiento de una muestra que fué oxidada, y
sobre la que se inmovilizó un segmento de cadena de ADN. El efecto de
corrimiento del espectro se produce únicamente en presencia del ADN
complementario (las figuras fueron tomadas de: S.Chan,
S. R. Horner, B.
L. Miller, and
P. M. Fauchet, Mat. Res. Soc. Symp. Proc. Vol. 638 ). Esta funcionalización de la superficie permite preparar
sensores muy específicos,
en particular sería posible inmovilizar en dispositivos de este tipo un
segmento de cadena de ADN asociado al Dengue, la Malaria u otras enfermedades de
importancia en la region, y obtener de esa manera sensores que permitan el
diagnóstico rápido de las mismas.
CUASICRISTALES....
Existe
un interés en el comportamiento fotónico de estructuras aperiódicas. El
espectro de Fourier correspondiente a un cristal periódico infinito perfecto
contiene funciones tipo delta centradas en números de onda correspondientes a
vectores de la red recíproca (este es el origen de la dispersión de Bragg).
Por el contrario, una estructura infinita aleatoria completamente desordenada
presenta un espectro de Fourier casi homogéneo. Existen como caso intermedio
estructuras aperiódicas, que presentan regularidades en el espectro de Fourier
y presentan pseudo-gaps. Estos son los denominados cuasicristales. Los
ejemplos más comunes de cuasicristales unidimensionales son los construidos en
base a las secuencias de Fibonacci y de Thue-Morse. Los espectros de Fourier de
los cuasicristales de Fibonacci presentan funciones delta, y los Thue-Morse
singularidades. Estas estructuras fotónicas son objeto actual de gran interés.
La estructura Thue-Morse se construye alternando las capas A y B con índices de
refracción nH y nL respectivamente y de espesor óptico deteminado siguiendo
una regla inductiva que permite obtener la estructura de orden (n+1) a partir de
la de orden n, sustituyendo A por AB y B por BA. Las estructuras Thue-Morse para
los primeros ordenes son: S 0 = A, S1 = AB, S2 = ABBA, S3 = ABBABAAB, etc.
La siguiente figura muestra el espectro de reflectancia de un cuasicristal.
Thue-Morse
S5, construida alternando capas A y B cada una de ellas con un espesor óptico
de 175 nm. Los índices de refracción son los mismos usados en las
microcavidades de las figuras anteriores.
Como puede verse, también en este caso las características del espectro
experimental coinciden bien con el espectro simulado. El espectro de esta
estructura contrasta con el de una única capa de silicio poroso principalmente
porque presenta bandas en las que la reflectancia alcanza casi el 100% como en
el caso de los reflectores de Bragg, mientras que la reflectancia máxima de una
única película sólo alcanza el 30 50 % dependiendo de la longitud de onda
(el valor máximo es la reflectancia de la superficie del silicio cristalino).
Este comportamiento muestra la presencia de bandas fotónicas prohibidas. Este
tipo de estructuras fotónicas permitirá estudiar efectos relacionados con el
comportamiento físico de las estructuras cuasicristalinas en general.
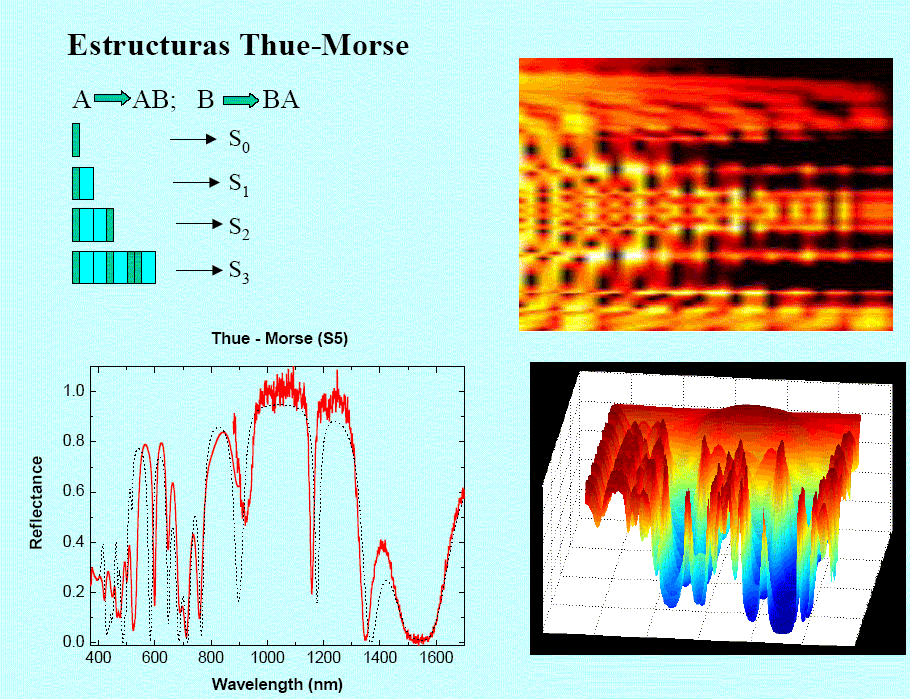
En
rojo: espectro de reflectancia de la estructura Thue-Morse S5, obtenida
según la secuencia cuyos primeros términos se indican a la izquierda.
El espesor óptico de cada capa es de 175 nm. La línea de puntos
corresponde al espectro simulado usando la matriz de transferencia óptica
del sistema. A la derecha arriba se muestra en escala de colores la
intensidad de campo en función de la energía y de la profundidad
óptica, en forma similar a una figura anterior. Abajo a la derecha,
gráfico 3D del coeficiente de transmisión óptica en función de la
energía y de la profundidad óptica.
|
PELÍCULAS
AUTOSOSTENIDAS...
En
el proceso de anodizado compiten procesos de transporte de carga y de masa, el
balance de los cuales determina las caracteristicas del ataque electroquímico.
Si la densidad de corriente es suficientemente grande, las irregularidades que
existen inicialmente en la superficie del electrodo de silicio se atenúan,
disolviendose las partes mas altas o cimas más rápidamente que las más
bajas o valles, de modo que se produce un electropulido. Si la densidad de
corriente es mas baja por el contrario, las irregularidades se profundizan y
aparece la estructura porosa. Además, el proceso es, como se dijo anteriormente
autolimitado, de modo que si se aplica un pulso de corriente de electropulido
luego de preparar una película u otro dispositivo fotónico este se separa del
sustrato sin que se altere la estructura del dispositivo o película. De este
modo se pueden hacer membranas autosostenidas.
En
las fotografías siguientes se observan tres muestras autosostenidas que fueron
transferidas a sustratos de vidrio. Son reflectores de bragg distribuidos,
todos ellos de 40 capas, con banda prohibida centrada en diferentes longitudes
de onda.
La
fotografía de la fila superior corresponde a las muestras iluminadas desde
arriba, de modo que se observa la reflexión de la luz en las mismas, mientras
que en la fila de abajo las muestras están interpuestas entre la fuente de luz
y la cámara, de modo que se observa la luz transmitida por las muestras. La
posibilidad de hacer muestras autosostenidas facilita el estudio de las mismas,
y permite hacer una variedad aun mayor de dispositivos fotónicos.












